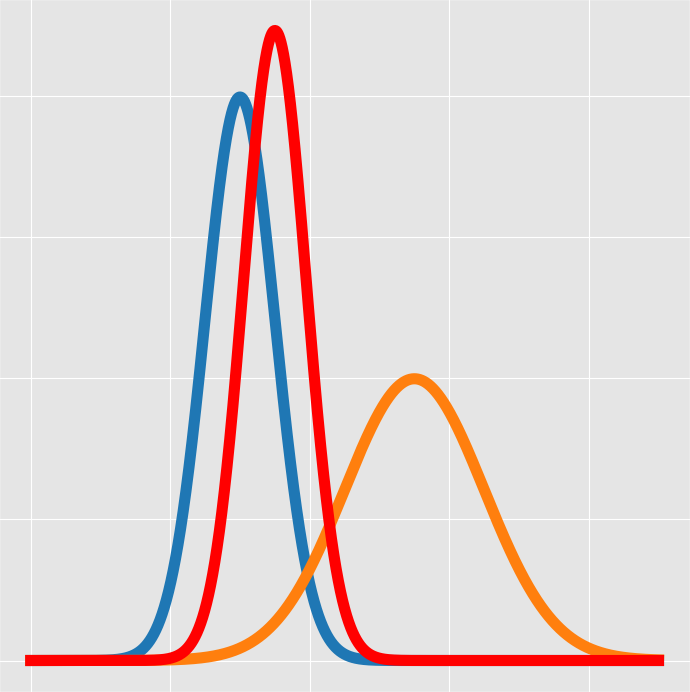
在贝叶斯推断中,后验分布与先验分布和似然之间存在一种重要的关系,即后验分布正比于先验分布乘以似然。这种关系可以通过贝叶斯定理来进行推导和解释。
贝叶斯定理:
贝叶斯定理描述了在观测到数据 $( D ) $后,参数 $( \theta )$ 的后验概率如何根据先验概率 $( P(\theta) )$ 和似然性函数 $( P(D|\theta) )$ 来更新。表达式如下:
$[ P(\theta|D) = \frac{P(D|\theta) \times P(\theta)}{P(D)} ]$
其中:
- $( P(\theta|D) )$ 是在给定观测数据 $( D )$ 后参数$ ( \theta )$ 的后验概率;
- $( P(D|\theta) )$ 是在给定参数 $( \theta ) $的条件下观测数据 $( D )$ 的似然性;
- $( P(\theta) )$ 是参数 $( \theta )$ 的先验概率;
- $( P(D) )$ 是数据 $( D )$ 的边际概率。
后验分布正比于先验分布乘以似然:
从贝叶斯定理中可以得出后验分布正比于先验分布乘以似然的结论,表达式如下:
$[ P(\theta|D) \propto P(D|\theta) \times P(\theta) ]$
这意味着后验分布与先验分布乘以似然性函数之间存在比例关系。具体解释如下:
- 先验分布 $( P(\theta) )$ 描述了在观测数据之前对参数 $( \theta )$ 的不确定性的初始估计;
- 似然性函数 $( P(D|\theta) ) $描述了在给定参数 $( \theta )$ 的情况下观测到数据 $( D )$ 的概率;
- 后验分布 $( P(\theta|D) )$ 结合了先验信息和新数据的信息,提供了在给定数据 $( D )$ 后对参数 $( \theta )$ 的更准确估计。
通过这种关系,我们可以利用先验知识和观测到的数据来更新对参数的估计,从而更好地理解数据和进行推断。这种贝叶斯方法在处理不确定性和小样本数据时非常有用。
卡尔曼滤波(Kalman Filter)是一种用于估计系统状态的数学算法,通过融合系统模型的预测信息和实际观测的测量信息,以优化对系统当前状态的估计。卡尔曼滤波算法的核心思想就是通过对系统状态的动态建模和不确定性的估计,来获得系统状态的最优估计。
具体来说,卡尔曼滤波通过以下步骤实现对当前状态的估计:
预测状态:首先根据系统的动态模型,利用系统的上一个状态值和系统的状态转移方程,预测系统的当前状态值。这一步是基于系统的内在规律进行的状态预测,不考虑观测值。
更新状态:接着,卡尔曼滤波考虑到当前的测量值,即观测到的系统状态值。通过比较实际观测值和预测状态值之间的差异,结合系统的测量方程和协方差矩阵,更新对系统当前状态的估计。这一步可以理解为根据测量结果对系统状态进行修正和优化,同时考虑到测量误差和系统动态的不确定性。
状态更新:经过预测和更新之后,卡尔曼滤波会根据预测和更新的结果来更新系统的状态估计和状态的不确定性,然后循环迭代这些步骤以获得对系统状态的连续估计。
总的来说,卡尔曼滤波算法充分利用了系统动态模型和传感器测量信息,通过预测和更新的步骤来获得对系统状态的最优估计。通过同时考虑上一个状态值和当前的测量值,卡尔曼滤波能够有效地处理系统动态、测量误差和不确定性,从而提高对系统状态的估计精度。
贝塞尔校正
在高斯分布(正态分布)中,如果我们从总体分布中抽取一小部分样本来估计总体的方差,通常情况下样本方差会低估总体方差。这种现象的原因主要是由于样本抽取的局限性和高斯分布概率密度函数的形状所导致的。
当我们从高斯分布中抽取样本时,由于高斯分布的中心值(均值)具有更高的概率密度,大部分样本会集中在均值附近,而在分布的尾部(边沿)位置上,样本数量相对较少。因此,如果我们只从高斯分布的中心值附近抽取样本来估计总体方差,由于未能很好地覆盖整个分布,很可能会导致总体方差的低估。
样本方差的计算是基于样本数据与样本均值之间的差异来衡量的。当样本主要集中在总体分布的中心值附近时,部分样本与样本均值之间的差异相对较小,导致样本方差的计算结果较小。而总体的方差是考虑了整个分布范围内数据点与总体均值之间的差异(包括边缘值),因此总体方差通常会大于样本方差。
因此,由于样本主要集中在高斯分布的中心值附近且样本数量有限,使用这部分样本来估计总体的方差往往会低估总体方差。为了更准确地估计总体方差,可以考虑增加样本数量、在整个分布范围内均匀抽样或者使用更复杂的统计方法来处理这种情况。

////////////////////////卡尔曼滤波器教程////////////////////////
k阶原点矩和k阶中心矩
在统计学中,k阶原点矩和k阶中心矩是用于描述概率分布特性的概念。
k阶原点矩:
对于一个随机变量X,它的k阶原点矩表示为μ_k = E(X^k),即该随机变量的k次幂的期望值。换句话说,k阶原点矩描述了随机变量X在k次幂上的平均值。k阶中心矩:
对于一个随机变量X,它的k阶中心矩表示为μ’_k = E[(X - μ)^k],其中μ为随机变量X的期望值(均值)。k阶中心矩是指将随机变量X减去其均值后再取k次幂的期望。换句话说,k阶中心矩描述了随机变量X关于均值的k次幂的期望值。
关于k阶原点矩和k阶中心矩的一些关键点:
- k阶原点矩包含数据的绝对信息,而k阶中心矩包含数据的相对信息。
- 一阶中心矩始终为0,因为它表示随机变量减去自身的均值,结果必然为0。
- 二阶中心矩是方差的平方根,用于衡量数据的离散程度。
- 三阶中心矩是偏度,用于衡量分布的对称性。
- 四阶中心矩是峰度,用于衡量分布的尖峭程度或平坦度。
总的来说,k阶原点矩和k阶中心矩是用于深入了解随机变量数据分布特性的重要统计量。它们提供了关于数据的高阶统计信息,能够帮助我们更全面地理解随机变量的性质和行为。
准度和精度
准度和精度是两个经常在科学与工程领域中使用的概念,它们表示了测量结果或数据的质量,但在含义上有所不同。
准度(Accuracy):
准度指的是测量结果或数据与真实数值之间的偏差程度,即测量结果的接近程度。如果测量结果与真实数值非常接近,则认为该测量是准确的,具有高准度。准度通常用误差或偏差来表示,可以是系统性的(偏差恒定)或随机性的(随机误差)。在实际应用中,准度的提高意味着更接近真实值的测量结果,即更少的误差。精度(Precision):
精度指的是多次测量所得结果之间的一致性或重复性,即测量结果的稳定程度。如果多次测量所得结果非常接近,可以认为该测量是精确的,具有高精度。精度通常用标准偏差或方差来描述,用来衡量测量数据的离散程度。在实际应用中,精度的提高意味着测量结果之间的一致性更高,即数据更加稳定。
区别总结:
- 准度强调测量结果与真实值之间的接近程度,而精度强调多次测量结果之间的一致性。
- 准度涉及测量结果的准确程度,精度涉及测量结果的稳定程度。
- 提高准度意味着减少与真实值的差距,而提高精度意味着增加测量结果之间的一致性。
在实际应用中,准确度和精度通常需要平衡考虑。一个测量既要准确地表达真实值,又要具有重复性和一致性,这样才能提供可靠的数据支持科学研究、工程设计等领域的决策和判断。
α−β−γ滤波器和卡尔曼滤波器的联系和区别
α-β-γ滤波器和卡尔曼滤波器都是用于估计系统状态的滤波器,它们有一些联系和区别:
联系:
- 两者都是常用的滤波器算法,用于估计系统的状态,并对传感器数据进行平滑处理。
- 在一定程度上,α-β-γ滤波器可以看作是卡尔曼滤波器的一种简化版本,适用于一些简单的系统。
区别:
- 卡尔曼滤波器是一种基于状态空间模型的递归滤波器,可以处理具有高斯噪声的动态系统。它通过状态估计和误差协方差估计来最优地结合先验信息和测量数据。相比之下,α-β-γ滤波器是一种更简单的滤波器,通常用于低成本的应用和对计算资源要求较低的场景。
- 在单个维度上,α-β-γ滤波器可用于对加速度数据进行滤波和平滑处理,而卡尔曼滤波器更常用于多维度状态估计,例如跟踪移动目标。
- 卡尔曼滤波器在处理非线性系统和非高斯噪声时效果更好,因为它能够自适应地调整协方差矩阵。而α-β-γ滤波器则更适用于线性系统或高斯噪声的情况。
总的来说,卡尔曼滤波器是一种更加通用和灵活的滤波器算法,适用于较为复杂的系统状态估计问题,而α-β-γ滤波器则是一种简单的滤波器算法,适用于一些简单的系统平滑处理任务。选择哪种滤波器取决于具体的应用场景和系统要求。
卡尔曼滤波
Q:
卡尔曼滤波是根据上一次的值得出的这一次的预测值和这一次的测量值这两个值加权求得的值吗
A:
卡尔曼滤波是一种用于估计系统状态的强大技术,确实涉及到对上一次状态的估计值、当前时刻的测量值和预测值进行加权平均。在卡尔曼滤波中,系统状态被表示为一个含有状态变量的向量,而系统的动态行为通常由一组线性动态方程和一组线性测量方程描述。
在每个时间步,卡尔曼滤波器执行以下两个主要步骤:
预测步骤(Predict):基于上一次的状态估计以及系统动态方程,预测系统的当前状态。这一预测考虑了上一次的状态估计和系统行为模型,产生一个预测的状态和协方差估计。
更新步骤(Update):将预测的状态与当前的测量值进行比较,根据二者的关系来修正预测状态,得到更准确的状态估计。这一步骤涉及卡尔曼增益的计算,以确保预测状态和测量状态之间的加权平均。
因此,在卡尔曼滤波中,通过将上一次的状态估计、当前时刻的预测值和测量值进行合理的加权组合,可以更好地估计系统的真实状态,并对噪声进行有效抑制。整个过程通过不断迭代预测和更新步骤,逐渐提高状态估计的准确性。