零基础实践深度学习(一):波士顿房价预测问题
Published in：2024-03-02 | category： 深度学习
Words: 9.2k | Reading time: 37min | reading：

波士顿房价预测问题

线性回归模型

数据处理

读入数据

1
2
3
4
5
6
7
# 导入需要用到的package
import numpy as np
import json
# 读入训练数据
datafile = './work/housing.data'
data = np.fromfile(datafile, sep=' ')
data

（我不知道为什么最后一行要加一个data）(好像他加一个data就不用print了？)
data = np.fromfile(datafile, sep=’ ‘):

  • 使用NumPy的 fromfile 函数来读取文件中的数据。
    • datafile 参数指定了要读取的数据文件的路径。
    • sep=' ' 参数表示数据在文件中是由空格分隔的。这意味着文件 housing.data 中的每一行都应该是由一系列由空格分隔的数值。
    • 读取的数据将被存储在一个NumPy数组中，并且赋值给变量 data。
      最后加上
      1
      print(data)
      在anaconda里运行一下：
      1
      2
      (Paddle_Py3.9) C:\Users\lxcqm>python "D:\opencv_test\demo\PythonApplication1\PythonApplication1\housing.py"
      [6.320e-03 1.800e+01 2.310e+00 ... 3.969e+02 7.880e+00 1.190e+01]

数据形状变换

由于读入的原始数据是1维的，所有数据都连在一起。因此需要我们将数据的形状进行变换，形成一个2维的矩阵，每行为一个数据样本（14个值），每个数据样本包含13个X（影响房价的特征）和一个Y（该类型房屋的均价）。

  • 读入之后的数据被转化成1维array，其中array的第0-13项是第一条数据，第14-27项是第二条数据，以此类推….
  • 这里对原始数据做reshape，变成N x 14的形式
    1
    2
    3
    4
    feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE','DIS', 
                     'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
    feature_num = len(feature_names)
    data = data.reshape([data.shape[0] // feature_num, feature_num])
    data = data.reshape([data.shape[0] // feature_num, feature_num]):

  1. data.shape[0]：这个部分是获取原始数据data的第一个维度的长度(获取行数)(当我们谈到数据集的长度时，我们通常指的是数据集中各个元素的数量，而不是字符的总数或字符字数)，也就是数据中元素的总数。[data.shape[1] 是用来获取数据集中的列数]对于一维数组（也称为向量），shape返回的是一个包含一个元素的元组，指示数组中元素的数量。这个值就是一维数组的长度。

  2. //：这是整数除法操作符，将两个数相除并返回整数部分，舍弃小数部分。此处是将数据总数除以特征数量，得到可以分成多少完整的样本集合。

  3. feature_num：这个值代表每个样本的特征数量，本例中是14个。

  4. [data.shape[0] // feature_num, feature_num]：这个部分定义了新的形状，将原始数据data重新组织为一个二维数组([行数，列数])，行数表示可以容纳完整样本集的数量，列数表示每个样本具有的特征数量。[] 中括号内的内容 [data.shape[0] // feature_num, feature_num] 表示的是一个包含两个值的列表

  5. 最终，data.reshape([data.shape[0] // feature_num, feature_num])通过这行代码将原始数据data按照新的形状重塑，每行包含一个完整的14个特征的样本数据，确保了数据集的完整性和规范性。

查看数据:

1
2
3
x = data[0]     //数据集的第一个样本
print(x.shape)  
print(x)

运行结果:

1
2
3
4
5
(Paddle_Py3.9) C:\Users\lxcqm>python "D:\opencv_test\demo\PythonApplication1\PythonApplication1\housing.py"
[6.320e-03 1.800e+01 2.310e+00 ... 3.969e+02 7.880e+00 1.190e+01]
(14,)
[6.320e-03 1.800e+01 2.310e+00 0.000e+00 5.380e-01 6.575e+00 6.520e+01
 4.090e+00 1.000e+00 2.960e+02 1.530e+01 3.969e+02 4.980e+00 2.400e+01]

(14,) 这样的形状表示一个包含一个元素的元组，该元素的值为 14。在这种情况下，这个元组表示的是一个一维数组，其长度为 14。这意味着样本或数组具有 14 个元素或特征。形状的表示方式是最后面一个’,’前面的数字，表明数组的维度。
因此，(14,) 表示数组是一个包含 14 个元素的一维数组。

(14,) 和 (14,1) 所表示的含义有些微妙的区别。 - (14,) 表示一个包含 14 个元素的一维数组，此时该数组是一个一维数组，维度为 1。 - (14,1) 表示一个包含 14 行、1 列的二维数组，因此该数组是一个二维数组，维度为 2，每行只有一个元素。 在数学表示和编程中，维度的不同有时会影响一些运算和处理，因此在处理数据时需要注意区分它们的含义。

数据集划分

将数据集划分成训练集和测试集，其中训练集用于确定模型的参数，测试集用于评判模型的效果。
在本案例中，我们将80%的数据用作训练集，20%用作测试集，实现代码如下。通过打印训练集的形状，可以发现共有404个样本，每个样本含有13个特征和1个预测值。

1
2
3
4
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]
training_data.shape

使用int()函数是为了确保offset是一个整数值
data[:offset]:

在Python中，冒号:通常用于切片（slice）操作，用来指定要从列表、字符串、元组等序列类型中提取的部分数据范围。在这种情况下，data[:offset]表示从序列data的开头开始一直切片直到offset之前的位置（不包括offset位置），即取出索引从0到offset-1的元素。这个操作可以用来生成一个新的子序列，其中包含了原始数据序列中从0到offset-1位置的元素。

运行结果:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(Paddle_Py3.9) C:\Users\lxcqm>python "D:\opencv_test\demo\PythonApplication1\PythonApplication1\housing.py"
[[6.32000e-03 1.80000e+01 2.31000e+00 ... 3.96900e+02 4.98000e+00
  2.40000e+01]
 [2.73100e-02 0.00000e+00 7.07000e+00 ... 3.96900e+02 9.14000e+00
  2.16000e+01]
 [2.72900e-02 0.00000e+00 7.07000e+00 ... 3.92830e+02 4.03000e+00
  3.47000e+01]
 ...
 [1.42362e+01 0.00000e+00 1.81000e+01 ... 3.96900e+02 2.03200e+01
  7.20000e+00]
 [9.59571e+00 0.00000e+00 1.81000e+01 ... 3.76110e+02 2.03100e+01
  1.21000e+01]
 [2.48017e+01 0.00000e+00 1.81000e+01 ... 3.96900e+02 1.97700e+01
  8.30000e+00]]
(404, 14)

数据归一化处理

对每个特征进行归一化处理，使得每个特征的取值缩放到0~1之间。这样做有两个好处：一是模型训练更高效，在本节的后半部分会详细说明；二是特征前的权重大小可以代表该变量对预测结果的贡献度（因为每个特征值本身的范围相同）。

测试样本归一化时用的是训练样本的最大值、最小值

1
2
3
4
5
6
7
8
9
# 计算train数据集的最大值，最小值
# axis=0:列（同类数据）
maximums, minimums = \
                     training_data.max(axis=0), \   
                     training_data.min(axis=0)
# 对数据进行归一化处理
# 像方差一样的思想，都对等到0-1之间的数（最大值是1，最小值是0）
for i in range(feature_num):
    data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])
\

在代码片段中，maximums, minimums = training_data.max(axis=0), training_data.min(axis=0) 这行代码使用了反斜杠 \ 作为换行符使用。这种方式在Python中被称为行连接符，它可以将一行代码分成多行来提高可读性。
在Python中，反斜杠 \ 通常用于指示语句在下一行继续。在这个例子中，maximums, minimums = \ 是从下一行的training_data.max(axis=0), \继续的开始。整行代码被分为两行写入，但解释器会将这两行连接在一起执行，就好像是单行代码一样。

axis

training_data.max(axis=0)是Pandas库中DataFrame对象的函数调用方法，用于计算DataFrame中每列的最大值。参数 axis=0 指定了沿着列的方向进行操作，也就是计算每列的最大值。这个方法会返回一个包含每列最大值的Series对象。
如果使用axis=1参数调用 training_data.max(axis=1)，那么是在DataFrame中沿着行的方向计算每行的最大值。这将返回一个包含每行最大值的Series对象。通过这种方法，可以找到每行数据中的最大值。

python中for循环 
1
2
3
a = [1, 3, 4, 5]
for i in a:
	print(i)

输出：

1
2
3
4
5
6
7
8
>>> a = [1, 3, 4, 5]
>>> for i in a:
...     print(i)
...
1
3
4
5

当代码 for i in a: 执行时，它实际上是在遍历列表 a 中的每个元素，并将每个元素的值依次赋给变量 i，然后执行循环体中的代码

python中range()函数

  • 函数作用
    range() 函数可创建一个整数列表，一般用在 for 循环中。

    1
    2
    3
    4
    5
    6
    7
    8
    >>> for i in range(5):
    ...     print(i)
    ...
    0
    1
    2
    3
    4

  • 函数语法
    range(start，stop[，step])

    参数说明：

    • start: 计数从 start 开始。默认是从 0 开始。例如range（5）等价于range（0， 5）;
    • stop: 计数到 stop 结束，但不包括 stop。例如：range（0， 5） 是[0, 1, 2, 3, 4]没有5
    • step：步长，默认为1。例如：range（0， 5） 等价于 range(0, 5, 1)
data[:i]和data[i:]和data[:，i]和data[i， :]
  • data[:i]：获取前i行的所有数据
  • data[i:]: 获取从i位置到末尾的所有数据
  • data[:, i]：获取第i列的所有数据（列号从第0列开始）
  • data[i, :]：获取第i行的所有数据（行号从第0行开始）
    data[:i]:第0行到第i-1行（不包括第i行）
    data[i:]:第i行到最后一行（包括第i行）

封装成load data函数

将上述几个数据处理操作封装成load data函数，以便下一步模型的调用

python中定义函数

不用声明~

1
2
3
4
5
6
def function_name(arguments):
    # 函数体，包括代码块
    # 可能包括返回语句

# 调用函数
result = function_name(argument_values)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
import numpy as np
import json


def load_data():
    # 导入数据
    datafile = "D:/paddlepaddle/housing/housing.data"
    data = np.fromfile(datafile, sep=' ')

    # 每条数据包括14项，其中前面13项是影响因素，第14项是相应的房屋价格中位数
    feature_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX',
                     'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO',
                     'B', 'LSTAT', 'MEDV']
    feature_num = len(feature_names)

    # 将原始数据进行Reshape，变成[N, 14]这样的形状
    data = data.reshape([data.shape[0] // feature_num, feature_num])

    # 将原始数据集拆成训练集和数据集
    # 这里使用80%的数据做训练，20%的数据做测试
    # 测试集和训练集必须是没有交集的
    ratio = 0.8
    offset = int(data.shape[0] * ratio)
    training_data = data[:offset]

    # 计算训练集每一列的最大值、最小值
    maximums, minimums = training_data.max(axis=0), training_data.min(axis=0)

    # 对数据进行归一化处理
    for i in range(feature_num):
        data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])

    # 训练集和测试集的划分比例
    test_data = data[offset:]
    return training_data, test_data


training_data, test_data = load_data()
x = training_data[:, :-1]
y = training_data[:, -1:]
print(x[0])
print(y[0])

  1. x = training_data[:, :-1]：
    这行代码会将 training_data 中所有行的除了最后一列（即特征变量）之外的所有列切片提取出来，赋值给变量 x。这意味着 x 包含了所有的特征变量。

  2. y = training_data[:, -1:]：
    这行代码会将 training_data 中所有行的最后一列（即目标变量）提取出来，赋值给变量 y。这意味着 y 包含了所有的目标变量。

教程写了两遍training_data = data[:offset]？不懂为什么
输出:

1
2
3
4
5
(Paddle_Py3.9) C:\Users\lxcqm>python "D:\opencv_test\demo\PythonApplication1\PythonApplication1\housing.py"
[0.         0.18       0.07344184 0.         0.31481481 0.57750527
 0.64160659 0.26920314 0.         0.22755741 0.28723404 1.
 0.08967991]
[0.42222222]

模型设计

模型设计是深度学习模型关键要素之一，也称为网络结构设计，相当于模型的假设空间，即实现模型“前向计算”（从输入到输出）的过程。
如果将输入特征和输出预测值均以向量表示，输入特征x有13个分量，y有1个分量，那么参数权重的形状(shape)是13×1。假设我们以如下任意数字赋值参数做初始化：
w=[0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,-0.1,-0.2,-0.3,-0.4,0.0]

详细解释

这些数字表示了初始化时每个输入特征对应的权重值。例如，第一个特征的权重是0.1，第二个特征的权重是0.2，以此类推。最后一个数字0.0是偏置项（bias），通常用来调整模型对数据的拟合情况。
在线性回归模型中，通过对输入特征和权重进行加权求和，并加上偏置项，来预测输出值。具体地，对于给定的输入特征向量x，输出值y可以通过以下方式计算得到：
y = w1x1 + w2x2 + … + w13*x13 + bias
将权重参数w与输入特征向量x的对应分量相乘并求和，再加上偏置项，就可以得到模型的预测输出值。

偏置项(bias)

偏置项（bias）在机器学习中是模型中的一个重要参数，通常用来在模型中引入偏移量，帮助模型更好地拟合数据。偏置项可以理解为模型中的截距，用来调整模型预测的基准值，即在没有输入特征时模型预测的值。

在线性回归模型中，偏置项可以帮助模型更好地拟合数据的整体偏移。考虑一个简单的二维线性回归模型，假设没有偏置项，模型预测是通过输入特征的加权和来计算的。如果数据在原点附近分布，模型可能能够较好地拟合数据。但如果数据出现偏移（即不再经过原点），没有偏置项的模型可能无法很好地捕捉到这种整体偏移。

通过引入偏置项，模型获得了一个额外的参数来平移整个预测结果，使其更贴合数据的整体分布情况。偏置项允许模型在不依赖输入特征的情况下做出一定的预测，从而更灵活地适应不同的数据集。

1
2
w = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, -0.1, -0.2, -0.3, -0.4, 0.0]
w = np.array(w).reshape([13, 1])
np.array(w).reshape([13

和开始的data.reshape的区别：

  1. data.reshape:

    • data.reshape 是对已经存在的数组 data 进行形状改变的操作，返回一个新的数组，原始数组 data 的形状并不会发生改变。这个方法适用于NumPy数组对象。
    • 示例：data = data.reshape([num_rows, num_cols])

  2. np.array(w).reshape:

    • np.array(w).reshape 则是将一个列表或其他类似对象 w 转换为NumPy数组，然后再对其进行形状改变操作。这个函数没有副作用，仅在返回新的数组时改变形状。
    • 示例：w = np.array(w).reshape([num_rows, num_cols])

如果已经有一个NumPy数组对象，且只需改变其形状而不需要创建新数组，可以直接使用 data.reshape。如果想将一个列表或其他类型对象转换为NumPy数组并改变其形状，则需要使用 np.array(w).reshape。

1
2
3
4
5
6
x1 = x[0]
t = np.dot(x1, w)
print(x1)
print(w)
print(t)

t = np.dot(x1, w)：

  • 这行代码将两个数组 x1 和 w 进行矩阵乘法运算，并将结果存储在变量 t 中。
  • np.dot 是 NumPy 提供的矩阵乘法函数，可以用于计算两个数组的点积（内积）。
    输出:
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    [0.         0.18       0.07344184 0.         0.31481481 0.57750527
     0.64160659 0.26920314 0.         0.22755741 0.28723404 1.
     0.08967991]
    [[ 0.1]
     [ 0.2]
     [ 0.3]
     [ 0.4]
     [ 0.5]
     [ 0.6]
     [ 0.7]
     [ 0.8]
     [-0.1]
     [-0.2]
     [-0.3]
     [-0.4]
     [ 0. ]]
    [0.69474855]
    行向量乘列向量

    行向量乘以列向量是一种矩阵乘法操作。具体来说，如果有一个行向量（1 x n）和一个列向量（n x 1），它们的维数在矩阵乘法中是匹配的，可以进行相乘操作。结果将会是一个标量（1 x 1 矩阵），即一个单独的数值。
    例如，如果有一个行向量 a = [a1, a2, …, an]（1 x n）和一个列向量 b = [b1, b2, …, bn]（n x 1），它们的乘积为：
    a * b = a1b1 + a2b2 + … + anbn
    因此，行向量乘以列向量的结果是这两个向量对应位置元素的乘积的和。希望这样的解释能够帮助你理解矩阵乘法的操作。如果还有其他问题，请随时告诉我。

完整的线性回归公式，还需要初始化偏移量b，同样随意赋初值-0.2。那么，线性回归模型的完整输出是z=t+b，这个从特征和参数计算输出值的过程称为“前向计算”。

1
2
3
d = -0.2
z = t + d
print(z)

输出:

1
[0.49474855]

将上述计算预测输出的过程以“类和对象”的方式来描述，类成员变量有参数w和b。通过写一个forward函数（代表“前向计算”）完成上述从特征和参数到输出预测值的计算过程，代码如下所示。

类和对象 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Person:
    def __init__(self, name, age):
        self.name = name
        self.age = age
    
    def greet(self):
        print(f"Hello, my name is {self.name} and I am {self.age} years old.")

# 创建对象实例
person1 = Person("Alice", 30)
person2 = Person("Bob", 25)

# 访问属性并调用方法
print(person1.name)  # 输出: Alice
person2.greet()  # 输出: Hello, my name is Bob and I am 25 years old.

print后的f:
在Python中，f 字符串（格式化字符串）是在字符串前缀加上f的一种特殊方法，称为 f-string。它允许在字符串中嵌入表达式，可以在大括号 {} 内部直接引用变量或表达式的值。
输出：

1
2
3
(Paddle_Py3.9) C:\Users\lxcqm>python D:\opencv_test\demo\PythonApplication1\PythonApplication1\testtttt.py
Alice
Hello, my name is Bob and I am 25 years old.

init:
在Python中，__init__ 是一个特殊的方法，用于在创建一个新对象时进行初始化操作。这个方法也被称为构造函数，负责初始化对象的属性。在类的定义中，如果你定义了 __init__ 方法，那么在实例化类时会自动调用这个方法。

下面是 __init__ 方法的详细解释：

  • self：self 是一个指向对象本身的引用。在类中的方法定义中，第一个参数通常为 self，用于表示类的实例。
  • name 和 age：这两个参数是在创建对象时传入的参数，用于初始化对象的属性。
  • self.name = name：这行代码将传入的 name 参数赋值给对象的 name 属性。通过这种方式，可以为每个对象设置不同的姓名。
  • self.age = age：这行代码将传入的 age 参数赋值给对象的 age 属性。同样，通过这种方式，可以为每个对象设置不同的年龄。

在上面的例子中， __init__ 方法负责初始化 Person 类的对象的 name 和 age 属性。当创建 Person 类的实例时，传入的 name 和 age 参数会被用来初始化对象的属性值。例如，person1 = Person("Alice", 30) 这行代码就创建了一个名为 “Alice”，年龄为 30 的 Person 类的实例。

1
2
3
4
5
6
7
8
9
10
11
12
class Network(object):
    def __init__(self, num_of_weights):
        # 随机产生w的初始值
        # 为了保持程序每次运行结果的一致性，
        # 此处设置固定的随机数种子
        np.random.seed(0)
        self.w = np.random.randn(num_of_weights, 1)
        self.b = 0.
        
    def forward(self, x):
        z = np.dot(x, self.w) + self.b
        return z

  1. class Network(object)：在 class Network(object): 中，object 表示 Network 类继承自 object 类，使得 Network 类是一个新式类。在 Python 3 中，可以简写为 class Network:，这样也会默认继承自 object 类

  2. np.random.seed(0)：设置随机数种子为0，这样可以保证每次运行程序得到的随机数是一样的，有助于结果的可重现性。

  3. self.w = np.random.randn(num_of_weights, 1)：利用Numpy的randn函数生成一个服从标准正态分布的随机数数组，形状为(num_of_weights, 1)，其中num_of_weights 是传入的参数，代表权重的数量。这些随机数将作为神经网络的权重参数，用于神经网络的学习和预测过程。

  4. self.b = 0.：将偏置参数b初始化为0，这个参数也将在网络的运算中起着重要的作用，用于调整模型的输出。

基于Network类的定义，模型的计算过程如下所示:

1
2
3
4
5
net = Network(13)
x1 = x[0]
y1 = y[0]
z = net.forward(x1)
print(z)

输出:

1
2
(Paddle_Py3.9) C:\Users\lxcqm>python D:\opencv_test\demo\PythonApplication1\PythonApplication1\housing.py
[2.39362982]

从上述前向计算的过程可见，线性回归也可以表示成一种简单的神经网络（只有一个神经元，且激活函数为恒等式）。这也是机器学习模型普遍为深度学习模型替代的原因：由于深度学习网络强大的表示能力，很多传统机器学习模型的学习能力等同于相对简单的深度学习模型。

训练配置

模型设计完成后，需要通过训练配置寻找模型的最优值，即通过损失函数来衡量模型的好坏。训练配置也是深度学习模型关键要素之一。

通过模型计算$x_1$表示的影响因素所对应的房价应该是$z$, 但实际数据告诉我们房价是$y$。这时我们需要有某种指标来衡量预测值$z$跟真实值$y$之间的差距。对于回归问题，最常采用的衡量方法是使用均方误差作为评价模型好坏的指标，具体定义如下：

$$Loss = (y - z)^2 (公式3)$$

上式中的$Loss$（简记为: $L$）通常也被称作损失函数，它是衡量模型好坏的指标。读者可能会奇怪：如果要衡量预测房价和真实房价之间的差距，是否将每一个样本的差距的绝对值加和即可？差距绝对值加和是更加直观和朴素的思路，为何要平方加和？ 损失函数的设计不仅要考虑准确衡量问题的“合理性”，通常还要考虑“易于优化求解”。至于这个问题的答案，在介绍完优化算法后再揭示。

在回归问题中，均方误差是一种比较常见的形式，分类问题中通常会采用交叉熵作为损失函数，在后续的章节中会更详细的介绍。对一个样本计算损失函数值的实现如下。

1
2
Loss = (y1 - z)*(y1 - z)
print(Loss)

输出:

1
[3.88644793]

因为计算损失函数时需要把每个样本的损失函数值都考虑到，所以我们需要对单个样本的损失函数进行求和，并除以样本总数$N$。
$$L= \frac{1}{N}\sum_{i=1}^N{(y_i - z_i)^2} (公式4)$$
在Network类下面添加损失函数的计算过程如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Network(object):
    def __init__(self, num_of_weights):
        # 随机产生w的初始值
        # 为了保持程序每次运行结果的一致性，此处设置固定的随机数种子
        np.random.seed(0)
        self.w = np.random.randn(num_of_weights, 1)
        self.b = 0.
        
    def forward(self, x):
        z = np.dot(x, self.w) + self.b
        return z
    
    def loss(self, z, y):
        error = z - y
        cost = error * error
        cost = np.mean(cost)
        return cost

cost = np.mean(cost):
np.mean(cost) 使用NumPy库中的 mean() 函数计算 cost 中所有元素的平均值，然后将这个平均值赋给 cost 变量
使用定义的Network类，可以方便的计算预测值和损失函数。需要注意的是，类中的变量x,w,b,z，error等均是向量。以变量x为例，共有两个维度，一个代表特征数量（值为13），一个代表样本数量，代码如下所示。

1
2
3
4
5
6
7
8
net = Network(13)
# 此处可以一次性计算多个样本的预测值和损失函数
x1 = x[0:3]
y1 = y[0:3]
z = net.forward(x1)
print('predict: ', z)
loss = net.loss(z, y1)
print('loss:', loss)

输出:

1
2
3
4
predict:  [[2.39362982]
 [2.46752393]
 [2.02483479]]
loss: 3.384496992612791

训练过程

上述计算过程描述了如何构建神经网络，通过神经网络完成预测值和损失函数的计算。接下来介绍如何求解参数$w$和$b$的数值，这个过程也称为模型训练过程。训练过程是深度学习模型的关键要素之一，其目标是让定义的损失函数$Loss$尽可能的小，也就是说找到一个参数解$w$和$b$，使得损失函数取得极小值。

我们先做一个小测试：如 图5 所示，基于微积分知识，求一条曲线在某个点的斜率等于函数在该点的导数值。那么大家思考下，当处于曲线的极值点时，该点的斜率是多少？


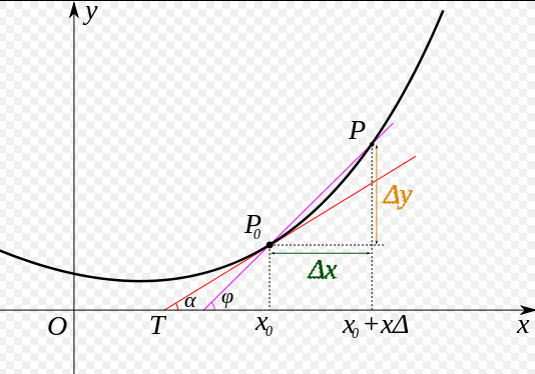
图5：曲线斜率等于导数值


这个问题并不难回答，处于曲线极值点时的斜率为0，即函数在极值点的导数为0。那么，让损失函数取极小值的$w$和$b$应该是下述方程组的解：
$$\frac{\partial{L}}{\partial{\boldsymbol{w}}}=0,(公式5)$$
$$\frac{\partial{L}}{\partial{b}}=0,(公式6)$$

其中$L$表示的是损失函数的值，$\boldsymbol{w}$为模型权重，$b$为偏置项。$\boldsymbol{w}$和$b$均为要学习的模型参数。

把损失函数表示成矩阵的形式为

$$
L=\frac{1}{N}||\boldsymbol{y}-(\boldsymbol{X}\boldsymbol{w}+\boldsymbol{b})||^2, (公式7)
$$

在公式中使用两个竖线 $|| \cdot ||$ 表示向量的范数（norm），具体来说，$||\boldsymbol{v}||$ 表示向量 $\boldsymbol{v}$ 的范数。在这个公式中，公式7中的 $||\boldsymbol{y} - (\boldsymbol{X}\boldsymbol{w} + \boldsymbol{b})||^2$ 表示向量 $\boldsymbol{y} - (\boldsymbol{X}\boldsymbol{w} + \boldsymbol{b})$ 的二范数的平方(二范数的平方等于内积)。二范数的计算方式是将向量中每个元素的平方相加，然后再开平方，而在这个公式中，我们直接对每个元素平方，即 $||\boldsymbol{v}||^2 = \sum_{i} v_i^2$。这个二范数的平方在线性回归中被用作损失函数的一部分，用来度量预测值和观测值之间的误差。

其中$\boldsymbol{y}$为$N$个样本的标签值构成的向量，形状为$N\times 1$；$\boldsymbol{X}$为$N$个样本特征向量构成的矩阵，形状为$N\times D$，$D$为数据特征长度；$\boldsymbol{w}$为权重向量，形状为$D\times 1$；$\boldsymbol{b}$为所有元素都为$b$的向量，形状为$N\times 1$。

计算公式7对参数$b$的偏导数
$$
\frac{\partial L}{\partial b} = \boldsymbol{1}^T(\boldsymbol{y}-(\boldsymbol{X}\boldsymbol{w}+\boldsymbol{b})), (公式8)
$$
请注意，上述公式忽略了系数$\frac{2}{N}$，并不影响最后结果。其中$\boldsymbol{1}$为$N$维的全1向量。

令公式8等于0，得到
$$
b^* = \boldsymbol{\bar{x}}^T\boldsymbol{w}-\bar{y}(公式9)
$$
其中$\bar{y}=\frac{1}{N}\boldsymbol{1}^T\boldsymbol{y}$为所有标签的平均值，$\boldsymbol{\bar{x}}=\frac{1}{N}(\boldsymbol{1}^T\boldsymbol{X})^T$为所有特征向量的平均值。将$b^*$带入公式7中并对参数$\boldsymbol{w}$求偏导得到

$$
\frac{\partial L}{\partial \boldsymbol{w}} = (\boldsymbol{X}-\boldsymbol{\bar{x}}^T)^T((\boldsymbol{y}-\bar{y})-(\boldsymbol{X}-\boldsymbol{\bar{x}}^T)\boldsymbol{w}) (公式10)
$$

令公式10等于0，得到最优参数

$$
\boldsymbol{w}^*=((\boldsymbol{X}-\boldsymbol{\bar{x}}^T)^T(\boldsymbol{X}-\boldsymbol{\bar{x}}^T))^{-1}(\boldsymbol{X}-\boldsymbol{\bar{x}}^T)^T(\boldsymbol{y}-\bar{y})(公式11) \
b^* = \boldsymbol{\bar{x}}^T\boldsymbol{w}^*-\bar{y}(公式12)
$$

将样本数据$(x, y)$带入上面的公式11和公式12中即可求解出$w$和$b$的值，但是这种方法只对线性回归这样简单的任务有效。如果模型中含有非线性变换，或者损失函数不是均方差这种简单的形式，则很难通过上式求解。为了解决这个问题，下面我们将引入更加普适的数值求解方法：梯度下降法。

梯度下降法

在现实中存在大量的函数正向求解容易，但反向求解较难，被称为单向函数，这种函数在密码学中有大量的应用。密码锁的特点是可以迅速判断一个密钥是否是正确的(已知$x$，求$y$很容易)，但是即使获取到密码锁系统，也无法破解出正确得密钥（已知$y$，求$x$很难）。

这种情况特别类似于一位想从山峰走到坡谷的盲人，他看不见坡谷在哪（无法逆向求解出$Loss$导数为0时的参数值），但可以伸脚探索身边的坡度（当前点的导数值，也称为梯度）。那么，求解Loss函数最小值可以这样实现：从当前的参数取值，一步步的按照下坡的方向下降，直到走到最低点。这种方法笔者称它为“盲人下坡法”。哦不，有个更正式的说法“梯度下降法”。

训练的关键是找到一组$(w, b)$，使得损失函数$L$取极小值。我们先看一下损失函数$L$只随两个参数$w_5$、$w_9$变化时的简单情形，启发下寻解的思路。
$$L=L(w_5, w_9) (公式13)$$
这里将$w_0, w_1, …, w_{12}$中除$w_5, w_9$之外的参数和$b$都固定下来，可以用图画出$L(w_5, w_9)$的形式，并在三维空间中画出损失函数随参数变化的曲面图。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
net = Network(13)
losses = []
# 只画出参数w5和w9在区间[-160, 160]的曲线部分，以及包含损失函数的极值
w5 = np.arange(-160.0, 160.0, 1.0)
w9 = np.arange(-160.0, 160.0, 1.0)
losses = np.zeros([len(w5), len(w9)])

# 计算设定区域内每个参数取值所对应的Loss
for i in range(len(w5)):
    for j in range(len(w9)):
        net.w[5] = w5[i]
        net.w[9] = w9[j]
        z = net.forward(x)
        loss = net.loss(z, y)
        losses[i, j] = loss

# 使用matplotlib将两个变量和对应的Loss作3D图
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()

# 如果您使用较新版本的matplotlib无法出图，可以替换为ax = fig.add_axes(Axes3D(fig))
ax = fig.add_axes(Axes3D(fig))

w5, w9 = np.meshgrid(w5, w9)

# 我加的，可以看出哪个轴对应哪个变量
ax.set_xlabel('w5')
ax.set_ylabel('w9')
ax.set_zlabel('Loss')

ax.plot_surface(w5, w9, losses, rstride=1, cstride=1, cmap='rainbow')
plt.show()

输出:

从图中可以明显观察到有些区域的函数值比周围的点小。需要说明的是：为什么选择$w_5$和$w_9$来画图呢？这是因为选择这两个参数的时候，可比较直观的从损失函数的曲面图上发现极值点的存在。其他参数组合，从图形上观测损失函数的极值点不够直观。

观察上述曲线呈现出“圆滑”的坡度，这正是我们选择以均方误差作为损失函数的原因之一。图6 呈现了只有一个参数维度时，均方误差和绝对值误差（只将每个样本的误差累加，不做平方处理）的损失函数曲线图。


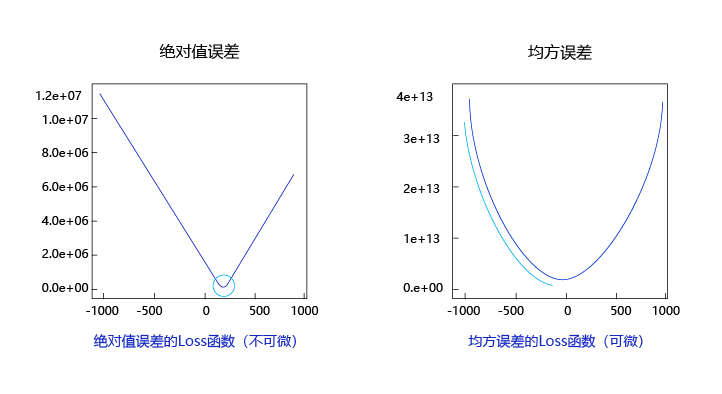
图6：均方误差和绝对值误差损失函数曲线图


由此可见，均方误差表现的“圆滑”的坡度有两个好处：

  • 曲线的最低点是可导的。
  • 越接近最低点，曲线的坡度逐渐放缓，有助于通过当前的梯度来判断接近最低点的程度（是否逐渐减少步长，以免错过最低点）。

而绝对值误差是不具备这两个特性的，这也是损失函数的设计不仅仅要考虑“合理性”，还要追求“易解性”的原因。

现在我们要找出一组$[w_5, w_9]$的值，使得损失函数最小，实现梯度下降法的方案如下：

  • 步骤1：随机的选一组初始值，例如：$[w_5, w_9] = [-100.0, -100.0]$
  • 步骤2：选取下一个点$[w_5^{‘} , w_9^{‘}]$，使得$L(w_5^{‘} , w_9^{‘}) < L(w_5, w_9)$
  • 步骤3：重复步骤2，直到损失函数几乎不再下降。

如何选择$[w_5^{‘} , w_9^{‘}]$是至关重要的，第一要保证$L$是下降的，第二要使得下降的趋势尽可能的快。微积分的基础知识告诉我们：沿着梯度的反方向，是函数值下降最快的方向，如 图7 所示。简单理解，函数在某一个点的梯度方向是曲线斜率最大的方向，但梯度方向是向上的，所以下降最快的是梯度的反方向。


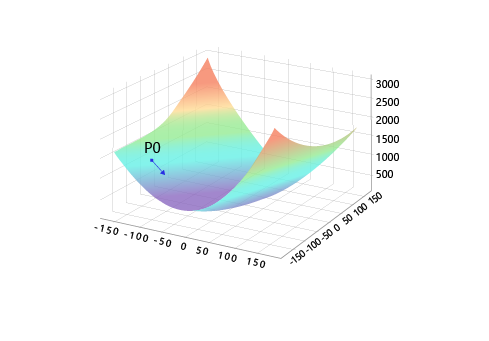
图7：梯度下降方向示意图


梯度计算

上文已经介绍了损失函数的计算方法，这里稍微改写。为了使梯度计算更加简洁，引入因子$\frac{1}{2}$，定义损失函数如下：

$$L= \frac{1}{2N}\sum_{i=1}^N{(y_i - z_i)^2} (公式14)$$

其中$z_i$是网络对第$i$个样本的预测值：

$$z_i = \sum_{j=0}^{12}{x_i^{j}\cdot w_j} + b (公式15)$$

在公式中，$(x_i^j)$ 中的 $(j)$ 表示输入样本的特征的索引。对于每个样本 $(i)$，有多个特征，其中特征索引为$(j)$ 从 0 到 12。这意味着每个样本 $(i)$ 包含了 13 个特征，用来描述或表示该样本的各个方面。因此，$(x_i^0, x_i^1, x_i^2, \ldots, x_i^{12})$ 分别表示第 $(i)$ 个样本的这 13 个特征的取值。在神经网络中，这些特征会与权重 $(w_j)$ 相乘，然后相加起来，从而得到对该样本的预测值 $(z_i)$

梯度的定义：

$$𝑔𝑟𝑎𝑑𝑖𝑒𝑛𝑡 = (\frac{\partial{L}}{\partial{w_0}},\frac{\partial{L}}{\partial{w_1}}, … ,\frac{\partial{L}}{\partial{w_{12}}} ,\frac{\partial{L}}{\partial{b}}) (公式16)$$

可以计算出$L$对$w$和$b$的偏导数：

$$\frac{\partial{L}}{\partial{w_j}} = \frac{1}{N}\sum_{i=1}^N{(z_i - y_i)\frac{\partial{z_i}}{\partial{w_j}}} = \frac{1}{N}\sum_{i=1}^N{(z_i - y_i)x_i^{j}} (公式17)$$

$$\frac{\partial{L}}{\partial{b}} = \frac{1}{N}\sum_{i=1}^N{(z_i - y_i)\frac{\partial{z_i}}{\partial{b}}} = \frac{1}{N}\sum_{i=1}^N{(z_i - y_i)} (公式18)$$

从导数的计算过程可以看出，因子$\frac{1}{2}$被消掉了，这是因为二次函数求导的时候会产生因子$2$，这也是我们将损失函数改写的原因。

下面我们考虑只有一个样本的情况下，计算梯度：

$$L= \frac{1}{2}{(y_i - z_i)^2} (公式19)$$

$$z_1 = {x_1^{0}\cdot w_0} + {x_1^{1}\cdot w_1} + … + {x_1^{12}\cdot w_{12}} + b (公式20)$$

可以计算出：

$$L= \frac{1}{2}{({x_1^{0}\cdot w_0} + {x_1^{1}\cdot w_1} + … + {x_1^{12}\cdot w_{12}} + b - y_1)^2} (公式21)$$

可以计算出$L$对$w$和$b$的偏导数：

$$\frac{\partial{L}}{\partial{w_0}} = ({x_1^{0}\cdot w_0} + {x_1^{1}\cdot w_1} + … + {x_1^{12}\cdot w_{12}} + b - y_1)\cdot x_1^{0}=({z_1} - {y_1})\cdot x_1^{0} (公式22)$$

$$\frac{\partial{L}}{\partial{b}} = ({x_1^{0}\cdot w_0} + {x_1^{1}\cdot w_1} + … + {x_1^{12}\cdot w_{12}} + b - y_1)\cdot 1 = ({z_1} - {y_1}) (公式23)$$

可以通过具体的程序查看每个变量的数据和维度。

1
2
3
4
5
6
x1 = x[0]
y1 = y[0]
z1 = net.forward(x1)
print('x1 {}, shape {}'.format(x1, x1.shape))
print('y1 {}, shape {}'.format(y1, y1.shape))
print('z1 {}, shape {}'.format(z1, z1.shape))

输出:

1
2
3
4
5
x1 [0.         0.18       0.07344184 0.         0.31481481 0.57750527
 0.64160659 0.26920314 0.         0.22755741 0.28723404 1.
 0.08967991], shape (13,)
y1 [0.42222222], shape (1,)
z1 [130.86954441], shape (1,)

按上面的公式，当只有一个样本时，可以计算某个$w_j$，比如$w_0$的梯度。

1
2
gradient_w0 = (z1 - y1) * x1[0]
print('gradient_w0 {}'.format(gradient_w0))

输出:

1
gradient_w0 [0.]

同样我们可以计算$w_1$的梯度。

1
2
gradient_w1 = (z1 - y1) * x1[1]
print('gradient_w1 {}'.format(gradient_w1))

输出:

1
gradient_w1 [23.48051799]

依次计算$w_2$的梯度。

1
2
gradient_w2= (z1 - y1) * x1[2]
print('gradient_w1 {}'.format(gradient_w2))

输出:

1
gradient_w1 [9.58029163]

聪明的读者可能已经想到，写一个for循环即可计算从$w_0$到$w_{12}$的所有权重的梯度，该方法读者可以自行实现。
我写哒->

1
2
3
for i in range(13):
    gradient_wi = (z1 - y1) * x1[i]
    print('gradient_w{} {}'.format(i, gradient_wi))

输出:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
(Paddle_Py3.9) C:\Users\lxcqm>python D:\opencv_test\demo\PythonApplication1\PythonApplication1\housing.py
gradient_w0 [0.]
gradient_w1 [0.35485337]
gradient_w2 [0.14478381]
gradient_w3 [0.]
gradient_w4 [0.62062832]
gradient_w5 [1.13849828]
gradient_w6 [1.26486811]
gradient_w7 [0.53070911]
gradient_w8 [0.]
gradient_w9 [0.44860841]
gradient_w10 [0.56625537]
gradient_w11 [1.9714076]
gradient_w12 [0.17679566]

使用Numpy进行梯度计算

基于NumPy广播机制（对向量和矩阵计算如同对1个单一变量计算一样），可以更快速的实现梯度计算。计算梯度的代码中直接用$(z_1 - y_1) \cdot x_1$，得到的是一个13维的向量，每个分量分别代表该维度的梯度。

NumPy广播机制
深度学习 paddlepaddle
Prev:
线性代数
Next:
蓝桥杯stm32学习笔记(四)：LCD液晶屏显示

    • Copyright © 2023 - 2024 tumytime | Powered by Hexo | Theme Bamboo

    Total visits： times |